The Ideal Gas in a Field: Transmembrane Ionic Gradients
Primary tabs
A Half-Step Beyond Ideal: Ion Gradients and Transmembrane Potentials
One key way the cell stores free energy is by having different concentrations of molecules in different "compartments" - e.g., extra-cellular vs. intracellular or in an organelle compared to cytoplasm. The molecules playing this role are charged molecules, or ions, such as sodium ($\plus{Na}$), chloride ($\minus{Cl}$), potassium ($\plus{K}$), calcium ($\dplus{Ca}$), and numerous nucleotide species. A brief overview of trans-membrane ion physiology is available.
Although the simplest way to study the physics of free energy storage in such a gradient is by considering ideal particles all with zero potential energy, the reality of the cell is that electrostatic interactions are critical. Fortunately, the most important non-ideal effects of charge-charge interactions can be understood in terms of the usual ideal particles (which do not interact with one another) that do, however, feel the effects of a "background" electrostatic field. Such a mean-field picture is a simple approximation to the electrostatic effects induced primarily by having an excess of one or more charged species on a given side of a membrane - for example, the excess of $\plus{Na}$ ions in the extracellular environment.
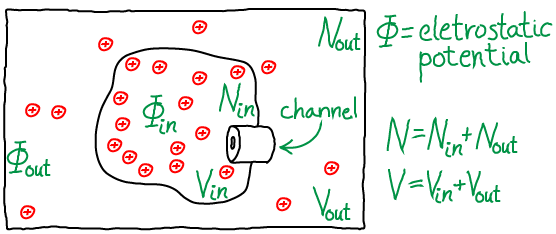
Two semi-ideal gases of ions in different potentials
Unlike our examination of two membrane-separated ideal gases, the particles here are explicitly charged and they "feel" the electrostatic potential $\Phi$. The positively charged anions schematically represent $\plus{K}$ ions interacting with the field generated by the imbalance of $\plus{Na}$ ions - the extracellular or "outside" concentration of sodium is maintained at a high value relative to the cytoplasm or "inside" by constant ATP-driven pumping. However, the effects of the $\plus{Na}$ concentration gradient will only be treated implicitly via the different values for $\inn{\Phi} < \out{\Phi}$.
To be precise, the model consists of $N$ particles that do not interact with one another, but which interact with the external potential $\Phi$ as if each had a charge of $q$, leading to potential energy $q \cdot \Phi_{\mathrm{X}}$ for each particle, where X = "in" or "out". The total volume $V$ is divided into inside and outside so that $\inn{V} + \out{V} = V$, with $\inn{N} + \out{N} = N$ ions populating the two compartments. The whole system is maintained at constant temperature $T$. Particles can pass through the channel shown in the figure, but we assume it is closed so that $\inn{V}$ and $\out{V}$ are constants: as shown in our discussion of two membrane-separated ideal gases, the assumption is a convenience and not an approximation because the total system volume $V$ and particle-number $N$ are truly constant.
Deriving the free energy
We have two gases of ideal "ions" (that interact with the external potential but not with other ions). Mathematically, we can largely follow our discussion of two membrane-separated ideal gases. The total free energy is the sum of the two ideal gas free energies and the two electrostatic potential energies:
 (1)
(1)where $\fidl$ is defined in the ideal gas page and $q$ is the ionic charge.
Substituting for $\fidl$ and noting that $\out{N} = N - \inn{N}$, we have
 (2)
(2)Because it is really the difference in electrostatic potential which governs the ionic behavior, we define $\dphi = \inn{\Phi} - \out{\Phi}$. In terms of this quantity, we can rewrite the total free energy as
 (3)
(3)
Eq. (3) is the free energy as a function of the number of particles inside the membrane (in volume $\inn{V}$). Inclusion of the electrostatic effects shifts the location of the most probable state, or free energy minimum.
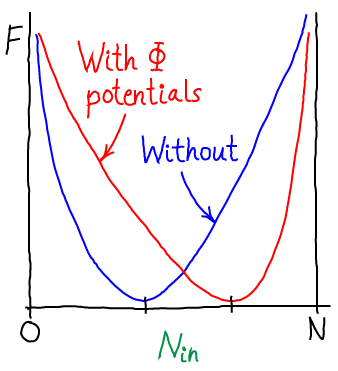
The most probable concentrations: The Nernst equation
If we open the channel and allow exchange of atoms between the compartments, the value of $\inn{N}$ can change. The probability of having $\inn{N}$ atoms in $\inn{V}$ is proportional to the Boltzmann factor of the free energy:
 (4)
(4)The most probable $\inn{N}$ value therefore can be found by determining the minimum of $F$. This will represent the equilibrium point in the thermodynamic limit (very large $N$ - when fluctuations about the most probable $\inn{N}$ will be very small compared to $\inn{N}$ itself). We set $\dee F / \dee \inn{N} = 0$ in Eq. (3), then re-arrange and cancel terms to find
 (5)
(5)Combining the terms using the rules of logarithms, followed by exponentiation, we find the Nernst equation,
 (6)
(6)where you should recognize the left-hand side as the ratio of concentrations.
In words, Eq. (6) shows that the concentrations inside and outside vary according to the Boltzmann factor of the ionic charge times the potential difference. Such an equilibrium is called a Donnan equilibrium. It should be comforting that when $\dphi = 0$, we recover equal concentrations.
Comparison to cellular behavior
As the exercise below will show, for some ions ($\minus{Cl}$, $\plus{K}$) the Nernst equation is a reasonable approximation. This suggests that such ions permeate the membrane passively. For some ions ($\plus{Na}$, $\dplus{Ca}$), the concentration ratios are very different from what would be predicted from the Nernst equation because the cell uses active transport to control them.
Mass action and its limitations
It is always worthwhile to pursue both thermodynamic and kinetic analyses of any system you really care about, or just to train yourself to consider a problem from multiple perspectives. By comparison to the present case, some of the results from the truly ideal (uncharged) two-compartment system may seem puzzling.
In contrast to the uncharged system, we can see that the transport rates through the channel cannot be equal in the two directions. Let $k_{io}$ be the inside-to-outside rate constant and $k_{oi}$ be the reverse rate constant. Starting from detailed balance, which says that the overall flows must be equal and opposite, and substituting the Nernst relation (6), we find that
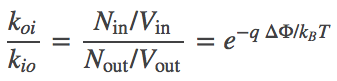 (7)
(7)
In other words, the ratio of rates for an ion channel depends on the potential difference. By itself, this does not contradict the mass action viewpoint (that rate constants are independent of concentrations) ... so long as $\dphi$ is truly constant. But if, more generally, $\dphi$ depends on the relative concentrations of the ion species moving through the channel, then the mass-action picture breaks down. Such a breakdown would occur, for example, if there were two species of ions, one of which could not permeate the membrane and hence was maintained at fixed inside and outside concentrations: in this case, flow of the permeable ion would change $\dphi$ and, in turn, change the rate "constants".
The brief overview of trans-membrane ion physiology may help to clarify the bigger picture of ion/membrane behavior.
References
- R. Phillips et al., "Physical Biology of the Cell," (Garland Science, 2009).
- B. Alberts et al., "Molecular Biology of the Cell", Garland Science (many editions available).
Exercises
- Derive Eqs. (5) and (6).
- Use Eq. (6) to derive a concentration ratio for $\minus{Cl}$ using $\dphi = -90 \, \mathrm{mV}$ (typical for skeletal muscle) and compare your result to the experimental value of $\sim 1 / 30$. This will require careful consideration of units when multiplying together physical constants.
